Las matemáticas son una disciplina que juega un papel importante en la resolución de problemas en todas las áreas de la vida. Su capacidad para traducir diversos fenómenos de la vida en lenguaje matemático lo convierte en una ciencia básica que todos deben dominar.
La relación entre un elemento del conjunto exactamente con un elemento de otro conjunto se llama función. En una función existe lo que se conoce como gráfico. Bueno, este gráfico de función muestra la relación matemática entre dos o más variables. Otra cosa que hay que saber es que en los componentes de relaciones y funciones conocemos Dominio, Dominio y Rango. Aquí hay una comprensión de los tres, tanto Dominio, Dominio y Rango.
Dominio
La definición de dominio es el área de origen o el conjunto que contiene el primer elemento del par ordenado de relación R.
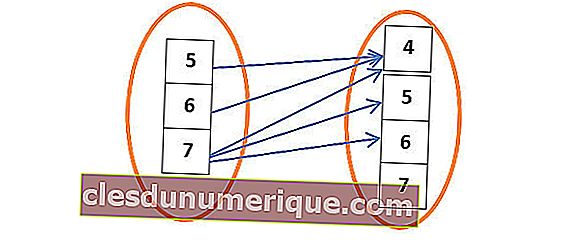
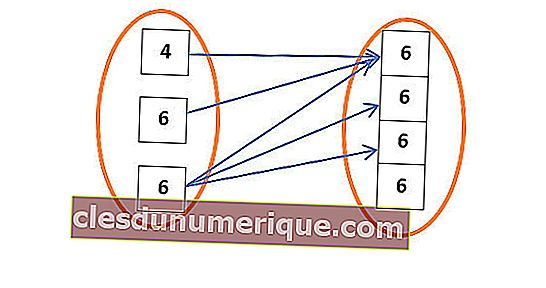
En el lado izquierdo está lo que se llama dominio. Entonces, todos los miembros incluidos en el círculo de la izquierda se llaman dominios, por lo que el dominio es 5,6,7.
(Lea también: Declaraciones y oraciones abiertas en matemáticas)
Codominio
El codominio es el área del conjunto amigo, o el conjunto que contiene los elementos del segundo conjunto de pares ordenados de relación R.
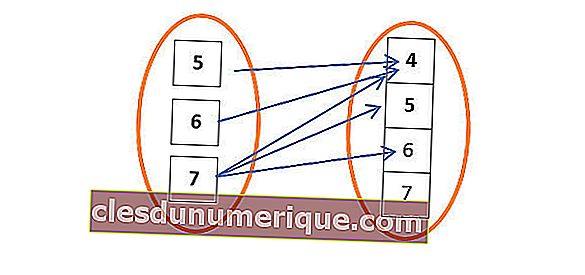
Para kodomain, esa es el área a la derecha. Todos los miembros de la derecha son miembros de los codominios, 4, 5, 6 y 7.
Rango
El rango es el área de resultado, o el conjunto de todos los miembros del conjunto B que tienen pares de miembros del conjunto A.
Ejemplo de problemas:
Sea R la relación A {1,2,3,4} con B {1,3,5}. R es una relación "x es menor que y" donde x es un miembro del conjunto A e y es un miembro del conjunto B. Entonces, ¿cuál es el dominio, codominio y rango de la relación R?
Solución:
Relación R en forma de un conjunto de pares ordenados:
R = ((1,3), (1,5), (2,3), (2,5), (3,5), (4,5)}
Entonces el dominio (R) o el primer elemento del par es (1,2,3,4)
En cuanto al dominio, el segundo elemento es (1,3,5)
Para el rango o miembros del conjunto B que han establecido el par A es (3,5)