¿Prestas atención, si el techo de la casa y la carpa tienen casi la misma forma? Si miras de nuevo, parece que consta de 2 triángulos en cada extremo, luego cubiertos con una manta que es rectangular. Esta forma también se conoce como prisma triangular. Se llama así porque la base y la tapa son triangulares. En geometría, estudiaremos la definición y fórmula de prismas triangulares. En esta ocasión también discutiremos varios ejemplos del problema para poder comprender mejor este material.
Un prisma es una forma que tiene una tapa y una base con una forma congruente de n lados, mientras que los lados verticales son rectangulares.
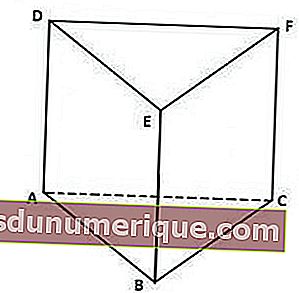
Los prismas triangulares tienen las siguientes características:
Tiene una base y una tapa triangulares congruentes.
De la imagen de arriba, la tapa del prisma, es decir, el triángulo DEF, tiene la misma forma y tamaño que el triángulo ABC como base.
Rectángulo como lado vertical.
Como puede ver, el prisma de arriba está limitado por tres rectángulos a cada lado de la vertical, es decir, los rectángulos ACFD, BCFE y ABED.
Tiene 5 lados, 9 aristas y 6 vértices.
Los 5 lados de un prisma triangular constan de 1 lado de la base, 1 lado de la tapa y 3 lados de la vertical. Mientras que las 9 costillas constan de 3 costillas verticales, 3 lados de la base y 3 lados de la tapa. Además, los 6 vértices son los puntos A, B, C, D, E y F.
Ahora que conocemos las características y también el significado de un prisma triangular, es hora de que conozcamos las fórmulas del prisma triangular y ejemplos de sus problemas.
Fórmulas de prismas triangulares y problemas de ejemplo
Habrá 2 tipos de fórmulas de prismas triangulares que aprenderemos. La fórmula para encontrar el volumen y la fórmula para encontrar el área de superficie. Las fórmulas son así:
Volumen
Para volumen, usaremos la fórmula:
V = área de la base × altura
o
V = (½ x a x h) × altura del prisma
Entonces, para entender esto mejor, veamos un ejemplo de este problema:
Un prisma mide 10 cm de alto. La base del prisma tiene la forma de un triángulo rectángulo con longitudes de lado de 4 cm y 3 cm, respectivamente. ¿Cuál es el volumen de este prisma triangular?
Solución:
Aquí, solo necesitamos insertar los números conocidos en una fórmula como esta:
V = (½ x a x h) × altura del prisma
V = (½ x 4 x 3) × 10
V = 6 × 10
V = 60 cm 3
Área de superficie
Al calcular el área de la superficie de un prisma triangular, usaremos una fórmula como esta:
L = (2 x área de la base) + (área de todos los lados perpendiculares)
si el triángulo es equilátero, entonces puedes usar la fórmula:
L = (2 x área de la base) + (3 x área de un lado de la vertical)
O podría ser la fórmula:
L = (2 x área de la base) + (perímetro de la base x altura del prisma)
Veamos un ejemplo de este problema para ver cómo se aplica esta fórmula. Aquí tienes un ejemplo del problema:
Hay un prisma triangular equilátero que tiene una altura de 12 cm, una longitud de lado de 5 cm y una altura de 8 cm. Entonces, ¿cuál es el área de la superficie de este prisma triangular?
Solución:
Para encontrar el área de superficie, simplemente usamos la fórmula para el área de superficie de un prisma triangular como este:
L = (2 x área de la base) + (3 x área de un plano vertical)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 cm 2
Así que esas son las diversas fórmulas de prismas triangulares que debe conocer, así como algunos ejemplos de problemas. Si aún está confundido, puede preguntar en la columna de comentarios, o puede probar Smart Class, la plataforma de tutoría en línea confiable en World.









