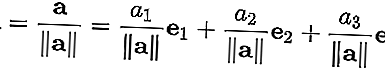El vector en matemáticas y física se puede definir como objetos geométricos que tienen magnitud y dirección. El vector está representado por una flecha, donde la base de la flecha muestra un punto de captura (punto de inicio) de un vector, la longitud de la flecha indica el tamaño o valor del vector (cuanto más larga es la flecha, mayor es el valor o valor del vector, y viceversa) , mientras que la flecha indica la dirección del vector.
Por escrito, si el vector comienza en el punto A y termina en el punto B, entonces se puede escribir en una letra pequeña encima de la cual hay una línea / flecha como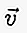 
o 
o 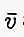también:
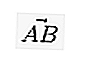
Tipos de vectores
El vector en matemáticas se divide en 4 tipos, que incluyen:
Vector de posición
Un vector cuyo punto de partida está en 0 (0,0) y su final es A (a1, a2).
Vector cero
"Vector cero" ( vector nulo o vector cero ) es un vector cuya longitud es "cero". Escribir en esta coordenada vectorial es (0,0,0), y generalmente se le da el símbolo 
, o 0 . Este vector se diferencia de otros vectores en que no se puede normalizar (es decir, ningún vector unitario es múltiplo del vector cero). La suma de los vectores cero con cualquier vector a es a (es decir, 0 + a = a ).
El vector cero no tiene una dirección clara del vector.
Vector unitario
es un vector de longitud "uno". Por lo general, los vectores unitarios solo se utilizan para indicar la dirección. Un vector de cualquier longitud se puede dividir por la longitud para obtener el vector unitario. Esto se conoce como "normalizar" un vector. Un vector unitario a menudo se indica con un "límite" sobre la "a" minúscula como en - .
Para normalizar un vector a = [ a 1 , a 2 , a 3 ], divida el vector por su longitud || a ||. Entonces:
Vector base
Un vector unitario que es perpendicular entre sí. En un espacio bidimensional, el vector ( R 2 ) tiene dos vectores base, a saber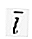 
= (1, 0) y 
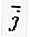= (0, 1).
Similitud de dos vectores
Se dice que dos vectores son iguales si tienen la misma longitud y dirección
Una alineación de dos vectores
Dos vectores se denominan paralelos (paralelos) si la línea que representa los dos vectores es paralela.
Operaciones vectoriales
Multiplicación escalar
Un vector se puede multiplicar por un escalar que da como resultado un vector también, el vector resultante es:
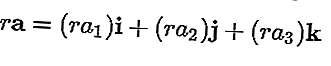
Suma y resta de vectores
Por ejemplo, los vectores a = a 1 i + a 2 j + a 3 k y b = b 1 i + b 2 j + b 3 k
El resultado de a más b es: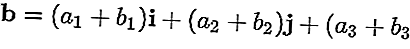 
La reducción de vectores también se aplica reemplazando el signo + por un signo -
