El círculo es un conjunto de puntos equidistantes de un punto. Las coordenadas de estos puntos están determinadas por la disposición de las ecuaciones circulares. Esto se determina en función de la longitud del radio y las coordenadas del centro del círculo.
En la imagen de arriba, podemos concluir que OP = OQ. El punto O se llama centro del círculo, mientras que OP y OQ son los radios. Consideremos el siguiente ejemplo.
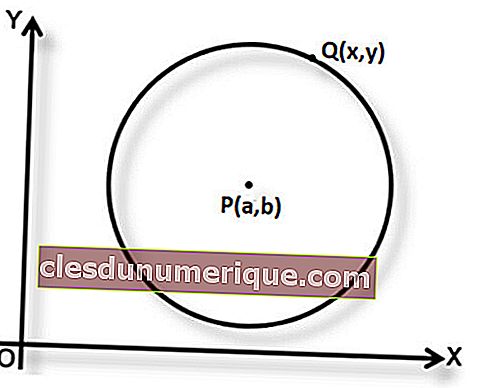
P (a, b) es el centro del círculo y la longitud del radio es r. Si Q (x, y) es un punto que se encuentra en el círculo, según la definición del círculo se puede concluir que PQ = r. A partir de esto, podemos formular la ecuación del círculo con P (a, b) como centro y r como radio.
√ (x - a) 2 + (y - b) 2 = r
(x - a) 2 + (y - b) 2 = r2
Trabajemos en un problema de ejemplo a continuación.
Encuentre la ecuación para el círculo cuyo centro está en el punto (-5,4) cuyo radio es 7.
De estos enunciados, sabemos que a = -5, b = 4 y r = 7. Si los conectamos a la ecuación, obtenemos la siguiente respuesta.
(x - (-5)) 2 + (y - 4) 2 = 72
(x + 5) 2 + (y - 4) 2 = 49
¿Qué tal un círculo cuya coordenada central está en P (0,0)? La ecuación del círculo es la siguiente.
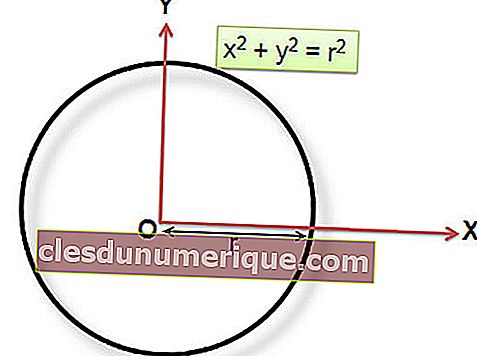
La forma general de la ecuación circular se puede expresar de las siguientes formas.
(x - a) 2 + (y - b) 2 = r2, o
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, o
X2 + y2 + Px + Qy + S = 0, donde P = -2a, Q = -2b y S = a2 + b2 - r2
Condiciones para determinar la ecuación de un círculo
La ecuación circular contiene tres variables arbitrarias. La ecuación circular se puede determinar si se conocen los valores de las tres variables. Para conocer los valores de estas tres variables, se debe cumplir una de las siguientes condiciones:
- Se conocen las coordenadas de los tres puntos del círculo.
- Se conocen las coordenadas de dos puntos del círculo conectados por el diámetro del círculo.
- Se conocen las coordenadas del punto central y las coordenadas del punto en el círculo.









