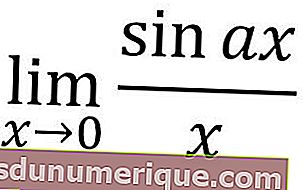El límite de la función trigonométrica se define como el valor más cercano a un ángulo en la función trigonométrica. Este cálculo se puede sustituir como el límite de una función algebraica, pero con una función trigonométrica que se debe cambiar primero.
La función trigonométrica debe convertirse en una identidad trigonométrica para un límite indefinido, que es un límite que, si se sustituye, será 0. Además, también existe una forma de calcular un límite indefinido sin usar la identidad trigonométrica, pero usando el teorema del límite trigonométrico. Otros usan tanto la identidad como el teorema simultáneamente.
Para determinar el valor límite de las funciones trigonométricas, se pueden utilizar varias formas, a saber, métodos numéricos, sustitución, factorización, tiempos de pares y derivadas.
(Lea también: Medición de la visibilidad mediante fórmulas trigonométricas)
Pero en función del valor, podemos dividir esta fórmula en dos, es decir, las que están cerca de un número y cerca de cero.
X acercándose a un número
Si tenemos el límite de la función trigonométrica cuya x se acerca al número c, podemos determinar su valor sustituyendo c en la función trigonométrica. Las fórmulas son las siguientes.

X acercándose a cero
Si la x del límite de una función trigonométrica se acerca a cero, podemos usar las fórmulas siguientes.

Si después de sustituir el valor de x en la función trigonométrica la forma indefinida es 0/0 ∞ / ∞, entonces para determinar el valor límite de la función trigonométrica, puede usar la regla de L'Hospital, a saber
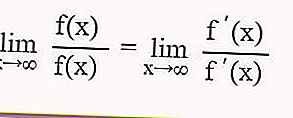
Comprensión intuitiva de los límites de las funciones de activación
Entender intuitivamente el límite de una función trigonométrica es lo mismo que el límite de una función algebraica. El límite de la función trigonométrica existe si y solo si existen el límite izquierdo y el límite derecho y el límite izquierdo es igual al límite derecho.