Si estudias matemáticas, debes haber escuchado o estudiado trigonometría. Bueno, la trigonometría es una rama de las matemáticas que estudia la relación entre el ángulo y las longitudes de los lados de un triángulo, como el seno, el coseno y la tangente. Tomado literalmente, la trigonometría proviene del griego, es decir, trigonon que significa "tres ángulos" y metron, que significa "medir". Al igual que con varios materiales de matemáticas, existen fórmulas trigonométricas que debe conocer.
En esta ocasión, intentaremos comprender varios tipos de fórmulas y también ejemplos de sus problemas.
Fórmulas trigonométricas
El concepto de trigonometría es un concepto importante en triángulos. Los valores trigonométricos se formulan en función de la relación de las longitudes de los lados de un triángulo rectángulo. Hay seis valores de razón trigonométrica, a saber, seno (sin), coseno (cos), tangente (tan), cosecante (cosec), secante (sec) y cotangente (cot). Los seis tipos de valores trigonométricos se pueden determinar comparando las longitudes de los lados con ciertas reglas.
Los usos de la trigonometría son muchos, que van desde la astronomía, la geografía, la teoría musical, la acústica, el análisis óptico del mercado financiero, la electrónica, la teoría de la probabilidad, la estadística, la biología, las imágenes médicas, la farmacia, la química y muchos más.
Entonces, ahora es el momento de que conozcamos las diversas fórmulas trigonométricas de esta lección.
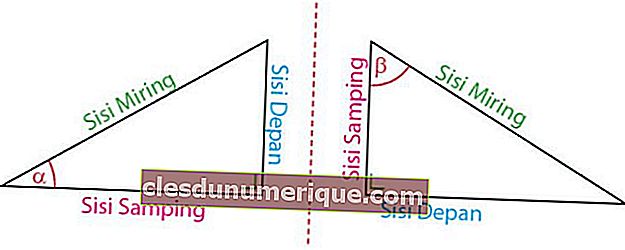
Fuente de la imagen: idschool.net
Según su ubicación con respecto al ángulo, los lados del triángulo - codo se dividen en tres tipos, a saber, el lado frontal, el lado lateral y la hipotenusa. El lado frontal es el lado que mira hacia la esquina. El lado está al lado de la esquina. El lado inclinado siempre está por delante del ángulo de 90o.
Bueno, las tres funciones trigonométricas principales son las funciones sin, cos y tan. La definición de las tres funciones basadas en los lados y ángulos de un triángulo rectángulo se puede ver en la figura y ecuación a continuación.
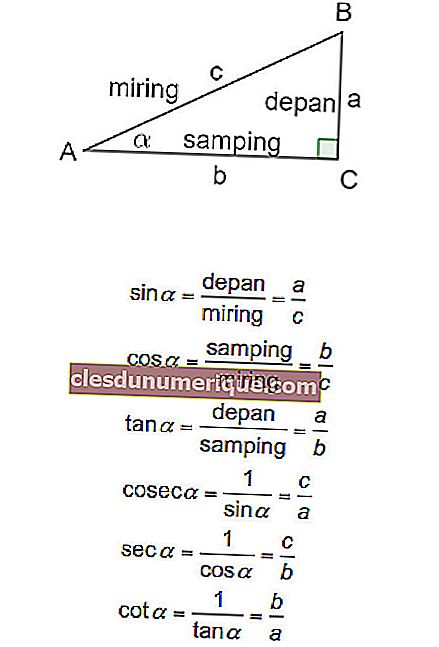
Ahora, específicamente para ángulos especiales, los valores trigonométricos son los siguientes:
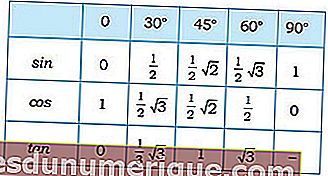
Fuente de la imagen: madematics.net
Comparación trigonométrica de ángulo correlacionado
La relación trigonométrica del ángulo relacionado es la extensión del valor trigonométrico básico que se determina a partir del ángulo del triángulo rectángulo. El ángulo de un triángulo rectángulo está solo en el cuadrante I porque es un ángulo agudo cuyo tamaño es 0 ° - 90 °.
El ángulo central del círculo está entre 0 ° y 360 °. El ángulo se divide en 4 cuadrantes, cada cuadrante tiene un rango de 90 °.
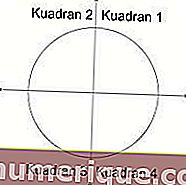
Fuente de la imagen: studiobelajar.com
- El cuadrante 1 tiene un ángulo entre 0 ° y 90 °. Todos los valores de razón trigonométrica son positivos en este cuadrante.
- El cuadrante 2 tiene un ángulo de entre 90 ° y 180 °. En este cuadrante, solo los valores de seno y cosecante son positivos.
- El cuadrante 3 tiene un ángulo de entre 180 ° y 270 °. En este cuadrante, solo las tangentes y las cotangentes son positivas.
- El cuadrante 4 tiene un ángulo entre 270 ° y 360 °. En este cuadrante, solo el coseno y la secante son positivos.
Identidad trigonométrica
El teorema de Pitágoras, es decir, a2 + b2 = c2, es la base para la preparación de identidades trigonométricas. Las identidades trigonométricas expresan la relación de una función trigonométrica con otras funciones trigonométricas.
La suma del seno al cuadrado y el coseno al cuadrado es igual a uno. Si ambos lados están divididos por el coseno al cuadrado, uno más la tangente al cuadrado es igual a la secante al cuadrado. Asimismo, si los dos lados están divididos por el seno al cuadrado, podemos obtener uno más la cotangente al cuadrado es igual a la cosecana al cuadrado.
Aquí está la fórmula de identidad:
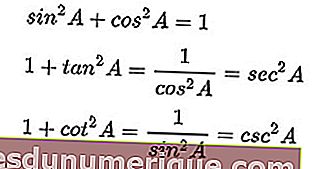
Fuente de la imagen: wikipedia.org
Varias otras fórmulas
Hay otra fórmula que debes conocer, a saber:
La fórmula para la suma y la diferencia de ángulos:
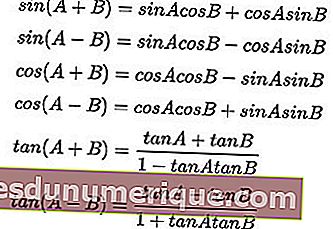
Fórmulas de multiplicación trigonométricas:
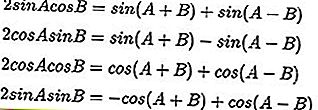
Fórmulas trigonométricas de suma y diferencia:
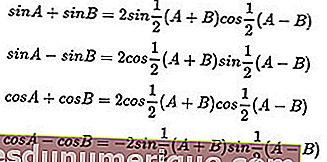
Ejemplos de problemas de activación
Halle el valor de 2 cos 75 ° cos 15 °:
Solución:
Con base en la información del problema, podemos ver que el problema anterior incluye multiplicaciones trigonométricas. Utilice la fórmula de multiplicación para cos descrita anteriormente, que es 2 cos A cos B = cos (A + B) + cos (A - B).
Responder:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
Esa es una colección de fórmulas y problemas trigonométricos que puede aprender y comprender. Para poder comprenderlo mejor, puede probar PROBLEM, una solución en línea ponderada y completa para practicar preguntas de acuerdo con el último plan de estudios de Smart Class. Desde la primaria, secundaria hasta secundaria con diversas materias como Matemáticas, Física, Química y otras. Aquí puede aprender varios tipos de fórmulas completas con problemas de ejemplo,
¡Vamos, qué estás esperando! Probemos ahora mismo los ejercicios PROBLEM en Smart Class.









