Para que lo sepas, las relaciones también existen en matemáticas, ¿sabes? Existen relaciones en el material con respecto a conjuntos. Las relaciones son reglas que conectan a los miembros de un conjunto con otros miembros del conjunto. La relación del conjunto A al conjunto B conecta a los miembros del conjunto A con los miembros del conjunto B. En esta oportunidad, aprenderemos sobre ejemplos de relaciones y sus propiedades, así como varios ejemplos de problemas que pueden ayudarlo a comprender mejor este material.
Ejemplos de relaciones y su naturaleza
La relación se puede definir como una regla que conecta a miembros del área de origen (dominio) y miembros de un área amiga (codominio). En una relación, no hay reglas especiales que deban cumplirse para emparejar a los miembros de la asociación regional con los miembros de las regiones amigas.
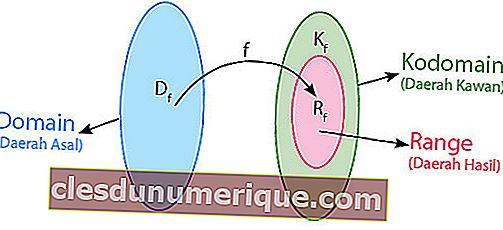
fuente: idschool.net
Cada miembro de la asociación regional de origen puede tener más de un socio o puede no tener ningún socio. La relación de dos conjuntos se puede expresar de tres formas, a saber:
- Diagrama de flechas
- Diagrama cartesiano.
- El conjunto de pares consecutivos
La siguiente es una explicación más detallada de las tres formas:
Gráficos de flechas
Los gráficos de flechas son la forma más fácil de expresar una relación. Este diagrama formará un patrón de relación en forma de flecha que muestra la relación entre los miembros del conjunto A y los miembros del conjunto B.
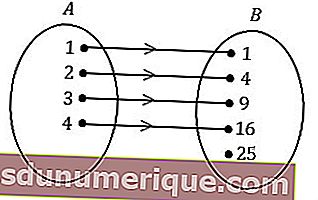
Fuente: maretong.com
Diagrama cartesiano
El diagrama cartesiano es un diagrama que consta de un eje X y un eje Y. En un diagrama cartesiano, los miembros del conjunto A están ubicados en el eje X, mientras que los miembros del conjunto B están en el eje Y. Las relaciones que conectan el conjunto A con B se indican mediante puntos o puntos.
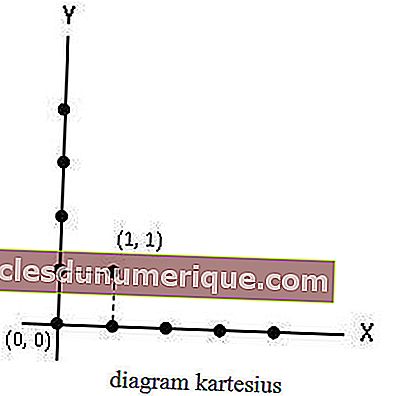
Conjunto de pares consecutivos
Una relación que conecta un conjunto con otro conjunto se puede representar en forma de un conjunto de pares ordenados. La forma de escribir es que los miembros del conjunto A se escriben primero, mientras que los miembros del conjunto B, que son los pares, se escriben en segundo lugar.
Ejemplos como este:
A = Conjunto mundial, Japón, Corea, Francia
Conjunto B = Tokio, París, Yakarta, Seúl
Determine el conjunto ordenado de pares por país y capital.
Responder:
{(Mundo, Yakarta), (Japón, Tokio), (Corea, Seúl), (Francia, París)}
Función
Una función o mapeo es una relación especial del conjunto A al conjunto B, con la regla de que cada miembro del conjunto A está emparejado exactamente uno con el miembro del conjunto B.
El resultado del mapeo de un dominio a otro se denomina rango de función o área de resultados. De manera similar a las relaciones, las funciones también se pueden representar en forma de diagramas de flechas, pares ordenados y diagramas cartesianos.
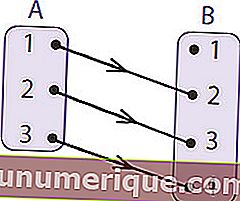
Fuente: rumushitung.com
Para comprenderlo mejor, considere la imagen de arriba. El conjunto A o área de origen se llama dominio. El conjunto B, que es un área amiga, se denomina codominio. El miembro del área amiga que es el resultado del mapeo se llama área de rendimiento o rango de funciones. Entonces, del diagrama de flechas de arriba se puede concluir que
- El dominio (D f) es A = {1,2,3}
- El codominio es B = {1,2,3,4}
- Rango / rendimiento (R f) es = {2,3,4}
Las funciones se pueden denotar con letras minúsculas como f, g, h, i, etc. La función f mapea el conjunto A con el conjunto B, luego se puede denotar por f (x): A → B.
Un ejemplo es la función f que asigna A a B con la regla f: x → 2x + 2. De la notación de la función, x es un miembro del dominio. La función x → 2x + 2 significa que la función f mapea x a 2x + 2. Entonces, el área de x por la función f es 2x + 2. Entonces puedes denotarlo como f (x) = 2x +2.
Si la función f: x → ax + b con x es un miembro del dominio f, entonces la fórmula para la función f es
f (x) = ax + b
Ejemplo de problemas:
Dada la función f: x → 2x - 2 donde x es un número entero. Intente determinar el valor de f (3).
Solución:
La función f: x → 2x - 2 se puede representar mediante f (x) = 2x - 2
entonces,
f (x) = 2x - 2
f (3) = 2 (3) - 2 = 4
Entonces ese es un ejemplo de relaciones y funciones en matemáticas. ¿Tiene alguna pregunta sobre esto? Escriba su pregunta en la columna de comentarios y no olvide compartir este conocimiento.









